Marching Cubes - Part 1 | Algorithm & Implementation
그럴듯한 절차생성 지형만들기!
Marching Cubes
Marching Cubes는 Scalar Field를 시각화 하기 위해 다각형 표면을 생성하는 알고리즘 입니다. 비슷한 알고리즘으로 이를 2차원에서 구현한 Marching Squares가 있죠. 따라서 대략적인 이해를 하고 싶은 분은 이전 글을(Marching Squares) 참고하면 좋습니다.
알고리즘의 동작
이 다음부터의 설명과 이미지들은 모두 Polygonise에 자세히 있습니다.
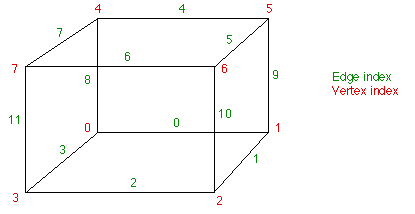모서리와 변에 대한 색인 규칙
알고리즘의 목표는 Scalar Field를 샘플링해 삼차원 격자에서 교차한 부분을 근사하여 찾고, 이를 이용해 Mesh를 만드는 것입니다. 만약 주어진 Scalar Field가 어떤 격자의 반만 교차한 상태라면, 격자의 반을 가르는 Quad를 만들게 됩니다.
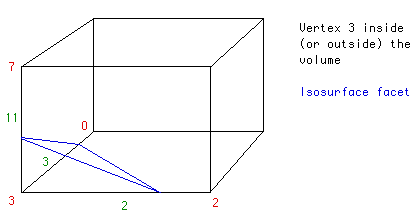3번 모서리가 교차된 상태
만약 3번 모서리만 교차된 상태라면 위 이미지와 같이 삼각형을 만들게 됩니다. 삼각형의 꼭짓점 위치는 0, 2, 3, 7번 모서리의 density 값에 관련하여 계산됩니다.
float[] densities = new float[8]; // 격자 모서리의 Density 값
int intersectionBits = 0;
for (int i = 0; i < 8; i++)
{
if (densities[i] > 0) // IsoValue는 0이라 가정
{
intersectionBits |= 1 << i;
}
}
만약 density가 0보다 크다면 해당 모서리는 교차되었다고 생각합니다. 예를들어 모서리가 모두 교차되었다면 intersectionBits는 11111111이 됩니다. 이를 EdgeTable의 Index로 사용해 어떤 변이 교차되었는지 알 수 있습니다.
static readonly int[] EdgeTable =
{
0x000, 0x109, 0x203, 0x30a, 0x406, 0x50f, 0x605, 0x70c, 0x80c, 0x905, 0xa0f, 0xb06, 0xc0a, 0xd03, 0xe09, 0xf00,
0x190, 0x099, 0x393, 0x29a, 0x596, 0x49f, 0x795, 0x69c, 0x99c, 0x895, 0xb9f, 0xa96, 0xd9a, 0xc93, 0xf99, 0xe90,
0x230, 0x339, 0x033, 0x13a, 0x636, 0x73f, 0x435, 0x53c, 0xa3c, 0xb35, 0x83f, 0x936, 0xe3a, 0xf33, 0xc39, 0xd30,
0x3a0, 0x2a9, 0x1a3, 0x0aa, 0x7a6, 0x6af, 0x5a5, 0x4ac, 0xbac, 0xaa5, 0x9af, 0x8a6, 0xfaa, 0xea3, 0xda9, 0xca0,
0x460, 0x569, 0x663, 0x76a, 0x066, 0x16f, 0x265, 0x36c, 0xc6c, 0xd65, 0xe6f, 0xf66, 0x86a, 0x963, 0xa69, 0xb60,
0x5f0, 0x4f9, 0x7f3, 0x6fa, 0x1f6, 0x0ff, 0x3f5, 0x2fc, 0xdfc, 0xcf5, 0xfff, 0xef6, 0x9fa, 0x8f3, 0xbf9, 0xaf0,
0x650, 0x759, 0x453, 0x55a, 0x256, 0x35f, 0x055, 0x15c, 0xe5c, 0xf55, 0xc5f, 0xd56, 0xa5a, 0xb53, 0x859, 0x950,
0x7c0, 0x6c9, 0x5c3, 0x4ca, 0x3c6, 0x2cf, 0x1c5, 0x0cc, 0xfcc, 0xec5, 0xdcf, 0xcc6, 0xbca, 0xac3, 0x9c9, 0x8c0,
0x8c0, 0x9c9, 0xac3, 0xbca, 0xcc6, 0xdcf, 0xec5, 0xfcc, 0x0cc, 0x1c5, 0x2cf, 0x3c6, 0x4ca, 0x5c3, 0x6c9, 0x7c0,
0x950, 0x859, 0xb53, 0xa5a, 0xd56, 0xc5f, 0xf55, 0xe5c, 0x15c, 0x055, 0x35f, 0x256, 0x55a, 0x453, 0x759, 0x650,
0xaf0, 0xbf9, 0x8f3, 0x9fa, 0xef6, 0xfff, 0xcf5, 0xdfc, 0x2fc, 0x3f5, 0x0ff, 0x1f6, 0x6fa, 0x7f3, 0x4f9, 0x5f0,
0xb60, 0xa69, 0x963, 0x86a, 0xf66, 0xe6f, 0xd65, 0xc6c, 0x36c, 0x265, 0x16f, 0x066, 0x76a, 0x663, 0x569, 0x460,
0xca0, 0xda9, 0xea3, 0xfaa, 0x8a6, 0x9af, 0xaa5, 0xbac, 0x4ac, 0x5a5, 0x6af, 0x7a6, 0x0aa, 0x1a3, 0x2a9, 0x3a0,
0xd30, 0xc39, 0xf33, 0xe3a, 0x936, 0x83f, 0xb35, 0xa3c, 0x53c, 0x435, 0x73f, 0x636, 0x13a, 0x033, 0x339, 0x230,
0xe90, 0xf99, 0xc93, 0xd9a, 0xa96, 0xb9f, 0x895, 0x99c, 0x69c, 0x795, 0x49f, 0x596, 0x29a, 0x393, 0x099, 0x190,
0xf00, 0xe09, 0xd03, 0xc0a, 0xb06, 0xa0f, 0x905, 0x80c, 0x70c, 0x605, 0x50f, 0x406, 0x30a, 0x203, 0x109, 0x000
};
앞서 봤던 이미지를 다시 예시로 3번 모서리만 교차되었다면, intersectionBits는 00001000(8)로 계산되고, EdgeTable[8]은 0x80c(1000 0000 1100)입니다. 즉, 2번 3번 11번 변이 교차되었다는 뜻이죠.
교차된 변을 알았으니 이를 이용해 삼각형을 만들 수 있습니다. 삼각형의 꼭짓점 위치는 간단한 선형 보간을 사용하여 구합니다.
결과
간단한 지형 생성기
Marching Cubes는 각 격자에 대해서 주변 격자와 상관없이 독립적으로 작동하기 때문에 병렬로 계산하기 좋습니다. 만약 Unity를 이용한다면 Job System을 사용하면 매우 좋은 퍼포먼스를 얻을 수 있죠. 저는 대략 15~20배 정도의 성능향상을 볼 수 있었습니다.
그럴듯한 절차생성!