Marching Squares - Part 1 | Algorithm
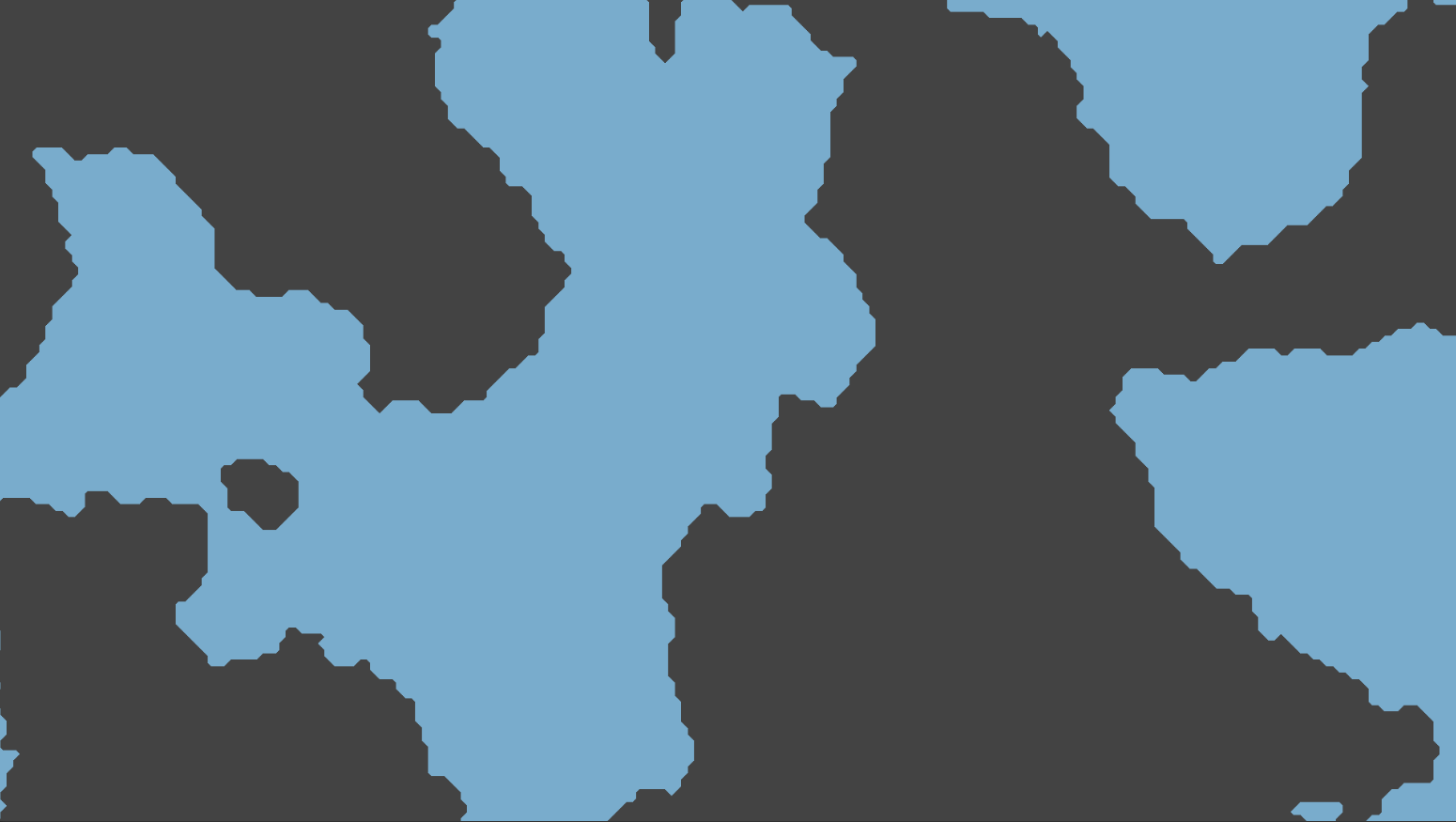 무엇이 땅이고 배경일까요??
무엇이 땅이고 배경일까요??
목차
- Marching Squares - Part 1 | Algorithm
- Marching Squares - Part 2 | Implementation
- Marching Squares - Part 3 | Optimization
Marching Squares
Marching Squares는 2D 공간상에서 Scalar Field에 대해서 윤곽선을 근사하여 만드는 알고리즘입니다. 이를 비슷하게 이용해 Mesh를 만들 수 있죠. 비슷한 알고리즘으로 3D 공간상에서 작동하는 알고리즘으로 Marching Cubes가 있습니다. 이는 나중에 다룰 예정입니다.
아래의 설명은 모두 구현과 관련된 설명입니다. 알고리즘의 일반적인 이야기는 위키(Marching_squares)에 자세히 나와있으니 참고하시면 좋습니다.
알고리즘의 동작
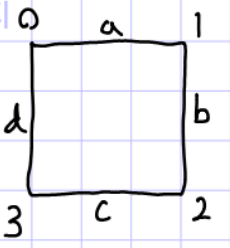 후에 a, b, c, d는 편의상 4, 5, 6, 7로 부르겠습니다.
후에 a, b, c, d는 편의상 4, 5, 6, 7로 부르겠습니다.
사각형의 각 모서리와 변을 순회하는 순서를 다음과 같이 사용하겠습니다. 각 모서리가 교차했는지 여부를 4개의 Bit로 표현할 수 있습니다. 이때 교차한 모서리의 순서를 4개의 Bit의 앞자리부터 매칭하여 생각합니다.
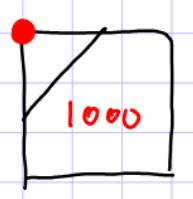 왼쪽 위 Corner가 교차된 상태
왼쪽 위 Corner가 교차된 상태
예를 들어 왼쪽 위 모서리만 교차되었다고 가정한다면 Bit는 1000입니다. 이렇게 해서 각 모서리가 교차하는 경우의 수를 생각하면 총 으로 총 16가지가 있습니다. 따라서 가능한 경우의 수를 모두 그려보면 다음과 같습니다.
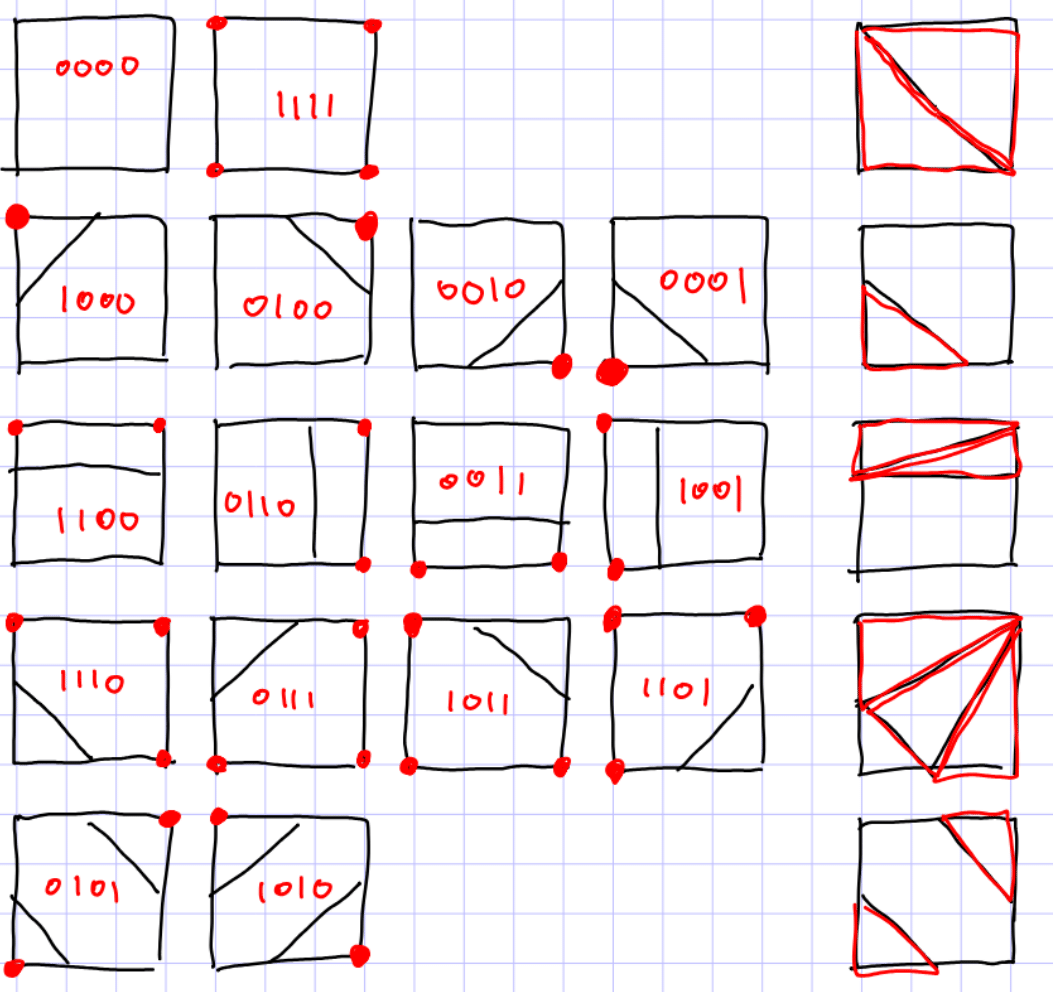 모서리가 교차할 수 있는 모든 경우의 수
모서리가 교차할 수 있는 모든 경우의 수
각 모서리에서 교차된 모서리를 빨간색 점으로 표현한 이미지입니다. 위 이미지에서 볼 수 있듯이 왼쪽 위, 아래 모서리를 사용한다고 했을 때, 이를 Bit로 표현하면 1001이 됩니다. 이 4개의 bit로 삼각형을 어떻게 만들어야 할지 결정하는 규칙을 정할 수 있습니다.
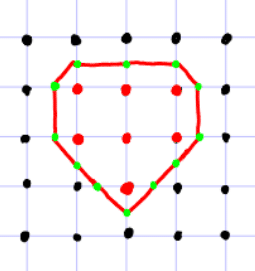 알고리즘의 동작 예시
알고리즘의 동작 예시
하지만 그 규칙을 사용하기 전에, 우선 격자로 나누어진 2차원 공간을 생각해봅시다. 각 격자의 꼭짓점마다 값이 있고, 이 값이 어떤 Threshold보다 높을 때, 그 꼭짓점이 교차된다고 생각합시다. 그렇다면 각 격자를 위에서 봤던 사각형이라고 생각한다면, 위 이미지를 어렵지 않게 생각할 수 있을 겁니다. 아주 단순한 알고리즘이죠.
또한 위 이미지를 자세히 보시면 초록색 점이 보이실 겁니다. 이는 각 격자에서 알고리즘에 의해 계산된 교차점입니다. 이 교차점을 기억해 나중에 삼각형을 만드는 데 사용합니다. 따라서 어떤 변이 교차되었는지 알 수 있도록 아래의 Table을 사용하겠습니다.
// Edge 규칙 Table
0, //{0, 0, 0, 0}, // 0000
3, //{0, 0, 1, 1}, // 0001
6, //{0, 1, 1, 0}, // 0010
5, //{0, 1, 0, 1}, // 0011
12, //{1, 1, 0, 0}, // 0100
15, //{1, 1, 1, 1}, // 0101
10, //{1, 0, 1, 0}, // 0110
9, //{1, 0, 0, 1}, // 0111
9, //{1, 0, 0, 1}, // 1000
10, //{1, 0, 1, 0}, // 1001
15, //{1, 1, 1, 1}, // 1010
12, //{1, 1, 0, 0}, // 1011
5, //{0, 1, 0, 1}, // 1100
6, //{0, 1, 1, 0}, // 1101
3, //{0, 0, 1, 1}, // 1110
0, //{0, 0, 0, 0}, // 1111
저는 앞서 Marching Cubes를 구현한 경험이 있으므로, 사전에 계산된 Table을 만들어 사용하기로 생각했습니다. 앞에서 계산한 모서리 교차 Bits를 인덱스로 받아 어떤 변이 교차되었는지 미리 계산해둔 Table입니다. 예를 들어 0011은 사각형의 아래 두 꼭짓점이 교차되었다는 뜻으로, Table에서 찾아보면 0101 = 5입니다. 이는 오른쪽과 왼쪽 변이 사용된다는 뜻이죠. 그리고 이 변의 교차점을 찾기 위해서는 보간을 사용하거나 변의 중심점을 사용합니다. 보간은 단순한 선형 보간을 사용합니다.
 왼쪽 : 선형 보간 / 오른쪽 : 중심점 사용
왼쪽 : 선형 보간 / 오른쪽 : 중심점 사용
하지만 여기서 끝난 건 아닙니다. Mesh를 만들기 위해서는 삼각형이 필요하기 때문이죠. 따라서 삼각형을 만드는 규칙도 필요합니다.
사실 Marching Squares를 구현할 때 이 알기 힘든 Table을 사용하지 않아도 구현할 수 있습니다. 하지만, 여기서 Table을 사용하는 이유는 물론 미리 계산되어있어 속도가 빠른 건 당연하지만, 앞으로 Marching Cubes를 구현할 때 비슷한 Table이 사용되기 때문입니다. Marching Cubes의 구현에서 겉보기엔 아주 길고 이해하기 힘든 Table을 사용하는데, 그때 사용하는 Table이 지금 소개하는 Table의 구조와 비슷합니다.
// 삼각형 규칙 Table
{-1, -1, -1, -1, -1, -1, -1, -1, -1}, // 0000
{3, 7, 6, -1, -1, -1, -1, -1, -1}, // 0001
{2, 6, 5, -1, -1, -1, -1, -1, -1}, // 0010
{3, 7, 5, 3, 5, 2, -1, -1, -1}, // 0011
{4, 1, 5, -1, -1, -1, -1, -1, -1}, // 0100
{4, 1, 5, 3, 7, 6, -1, -1, -1}, // 0101
{6, 4, 1, 6, 1, 2, -1, -1, -1}, // 0110
{2, 3, 7, 2, 7, 4, 2, 4, 1}, // 0111
{7, 0, 4, -1, -1, -1, -1, -1, -1}, // 1000
{3, 0, 4, 3, 4, 6, -1, -1, -1}, // 1001
{7, 0, 4, 2, 6, 5, -1, -1, -1}, // 1010
{3, 0, 4, 3, 4, 5, 3, 5, 2}, // 1011
{7, 0, 1, 7, 1, 5, -1, -1, -1}, // 1100
{0, 1, 5, 0, 5, 6, 0, 6, 3}, // 1101
{1, 2, 6, 1, 6, 7, 1, 7, 0}, // 1110
{3, 0, 2, 2, 0, 1, -1, -1, -1} // 1111
마지막으로 위에서 계산된 모서리 교차 Bit들과 변 교차 Bit들로 삼각형을 만드는 규칙 Table 입니다. 앞서 만들어진 4개의 모서리 교차 Bit를 다시 정수로 생각하면 그 범위는 0(0000)부터 15(1111)까지 입니다. 이를 Index로 이용해 위 Table의 첫 번째 행은 0000의 삼각형 규칙이고, 15번째 행은 1111의 삼각형 규칙으로 Table을 만들었습니다. 삼각형 규칙 Table에서는 -1부터 7까지의 정수를 이용하는데, 그 숫자의 의미는 아래 이미지에 있습니다.
사실 여기서 사용된 모든 Table은 직접 손으로 계산해서 만들었습니다. 따라서 잘못된 동작이나 오류가 확인된다면 언제든 저에게 알려주세요!
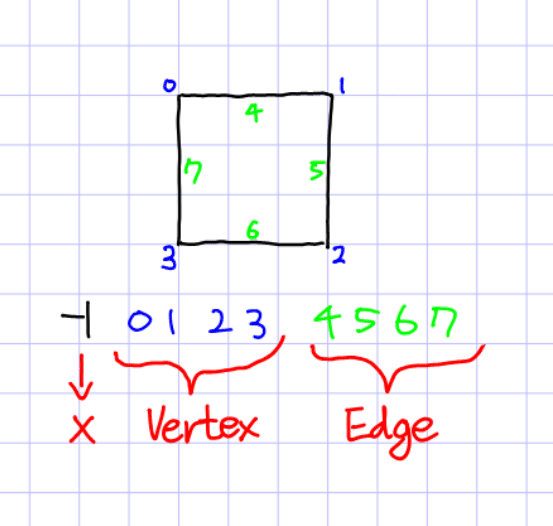
-1은 더이상 만들 삼각형이 없다는 뜻입니다. 0부터 3까지는 사각형의 모서리를 뜻하고, 4부터 7은 앞서 기억한 각 격자에서 변의 교차점을 뜻합니다. 예를 들어 5는 1과 2를 꼭짓점으로 하는 변이 교차되었다는 뜻입니다. 삼각형 규칙 Table에서 0110 Index를 예로 들면 삼각형은 2개로 꼭짓점을 641과 612로 사용하겠다는 뜻입니다. 여기서 4와 6은 위와 아래 변으로 변 자체를 쓰겠다는 의미가 아니라 변에서 교차된 점을 꼭짓점으로 사용하겠다는 뜻입니다.
위 테이블에서 -1은 의미가 없는 숫자이므로 빈 공간이라 생각하면, 위 테이블을 자세히 보시면 숫자가 3의 배수로 있다는 사실을 알 수 있습니다. 이는 당연히도 위 테이블은 삼각형을 만드는 규칙 Table이고, 삼각형은 3개의 꼭짓점을 가지고 있으니 그런 것이죠. 사실 당연한 이야기를 반복해서 했습니다.
마지막으로 정리한 알고리즘의 수도코드는 다음과 같습니다.
for all cells in grid:
densities = GetGridDensities() // 사각형에서 각 꼭짓점의 Density 값을 받아옴
intersectionBits = CalculateIntersectionBits(densities) // 꼭짓점의 교차된 점 계산 ex) 0010
edgeBits = EdgeTable[intersectionBits] // 어느 변이 교차되었는지 계산 ex) 0110
interpolatedPoints = InterpolateEdgePoints(edgeBits)
finalPoints = [corners, interpolatedEdges] // 사각형의 각 꼭짓점과 보간된 변의 교차점들을 합친 배열
while TriangleTable[intersectionBits, Index] != -1:
MakeTriangle()
모호성
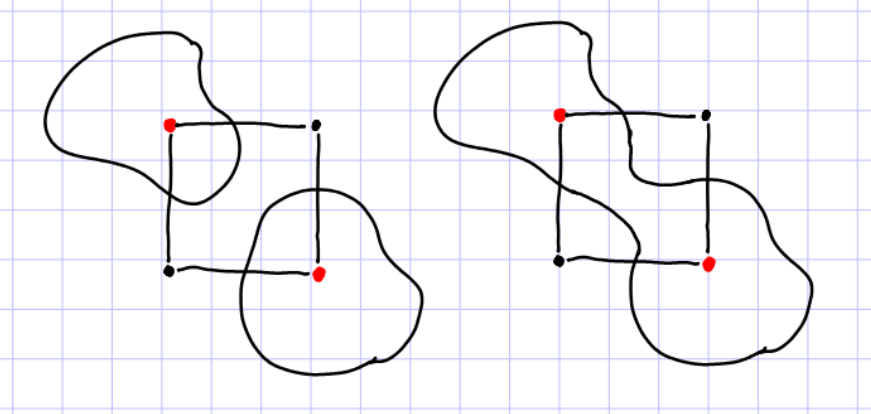 과연 삼각형을 어떻게 만들어야할까요?
과연 삼각형을 어떻게 만들어야할까요?
Marching Squares는 겉보기에는 잘 동작할 것 같지만, 위 이미지처럼 모호한 경우가 있습니다. 사실 이러한 예외는 2D Mesh를 생성하는 데에 있어서 실제로 오류는 아닙니다. 가장자리를 닫힌 상태로 만들든, 서로 연결되게 만들든 결국 모든 변이 닫힌(Closed) 상태이기 때문에 상황에 맞게 알고리즘을 작성하면 됩니다. 저는 위의 경우에서 서로 만나지 않게 처리를 했습니다.
마무리
이번 파트는 Marching Squares 알고리즘의 대략적인 동작을 알아보았습니다. 실제 구현은 다음 파트에서 다루겠습니다.
감사합니다.
