Marching Squares - Part 3 | Optimization
한번 옆으로 끌어보세요!
목차
- Marching Squares - Part 1 | Algorithm
- Marching Squares - Part 2 | Implementation
- Marching Squares - Part 3 | Optimization
VBO Indexing
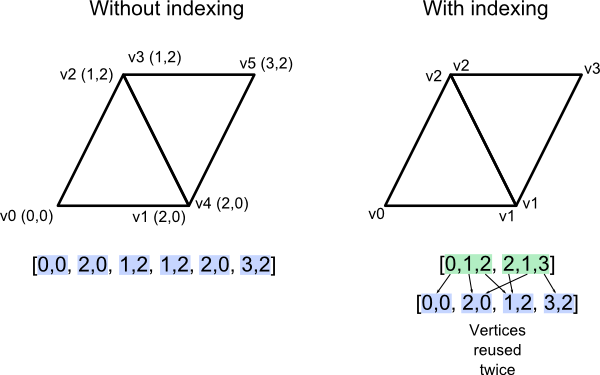중복된 정점 v2, v3와 v1, v4를 v2, v1으로 병합
지금까지, Metaball을 렌더링 하기 위해 Mesh를 만들 때, 삼각형을 만들 때마다 같은 정점을 공유하는 삼각형이 있음에도 불구하고 중복된 정점을 사용했습니다. 이를 해결하기 위해 VBO Indexing을 이용하여 불필요한 Vertex를 줄일 수 있습니다.
구현
Dictionary<Vector3, int> vertices; // 존재하는 정점들 <정점, 인덱스>>
if (vertices.ContainsKey(newVertex)) // 추가하려는 정점이 이미 존재한다면
{
triangles.Add(vertices[newVertex]);
}
else // 추가하려는 정점이 새로운 정점이라면
{
int vertexIndex = vertices.Count;
vertices.Add(newVertex, vertexIndex);
triangles.Add(vertexIndex);
}
결과
VBO Indexing 결과
들인 노력에 비해 정점의 수가 눈에 띄게 감소하였지만, 아직도 최적화 할 수 있는 여지가 있습니다.
Greedy Meshing
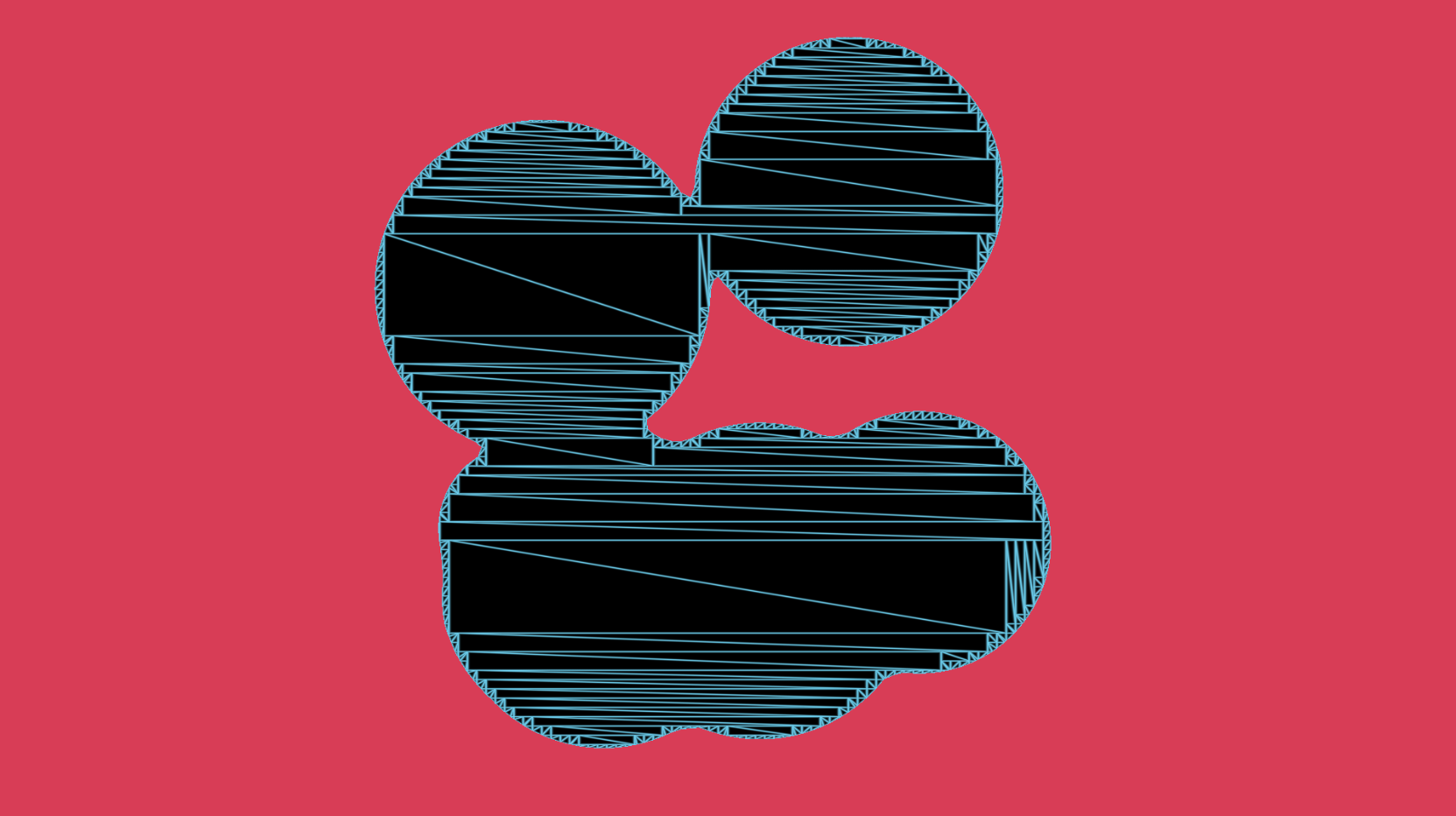Greedy Meshing 예시
Mesh를 최적화 할 수 있는 방법중에 하나인 Greedy Meshing 입니다. 위에 스크롤바를 이리저리 돌려보시면 Mesh를 Quad로 최적화 되었다는 사실을 알 수 있습니다. 사실 이는 Minecraft와 같이 Voxel형태의 Mesh를 다루는 게임 등에서 많이 사용되고 있는 방식입니다. 즉, Grid나 Voxel 형태처럼 완전한 Quad 또는 Cube 들을 병합하는 알고리즘입니다.
이름에서도 알 수 있듯이 이 알고리즘은 느리지 않고, 그럴듯하게 정점 수를 줄여줍니다. 알고리즘에 대한 자세한 내용은 0fps - Meshing in a Minecraft Game에서 확인할 수 있습니다.
구현
bool[,] quadMap; // 현재 Cell이 Quad인지 저장해둔 배열
for (int x = 0; x < chunkSize.x; x++)
{
for (int y = 0; y < chunkSize.y;)
{
Vector2Int gridPosition = new Vector2Int(x, y);
if (!quadMap[x,y])
{
y++;
continue;
}
// 높이 계산
int height = 0;
for (int dy = gridPosition.y; dy < chunkSize.y; dy++)
{
Vector2Int subGridPosition = new Vector2Int(gridPosition.x, dy);
if (!quadMap[subGridPosition.x, subGridPosition.y])
{
break;
}
height++;
}
// 넓이 계산
int width = 1;
bool done = false;
for (int dx = gridPosition.x + 1; dx < chunkSize.x; dx++)
{
for (int dy = gridPosition.y; dy < gridPosition.y + height && dy < chunkSize.y; dy++)
{
Vector2Int subGridPosition = new Vector2Int(dx, dy);
if (!quadMap[subGridPosition.x, subGridPosition.y])
{
done = true;
break;
}
}
if (done)
{
break;
}
width++;
}
// 사용한 quadMap 삭제
for (int dx = gridPosition.x; dx < gridPosition.x + width; dx++)
{
for (int dy = gridPosition.y; dy < gridPosition.y + height; dy++)
{
quadMap[dx, dy] = false;
}
}
// width height 만큼 Quad 생성
Vector2Int size = new Vector2Int(width, height);
Vector3[] quad = new Vector3[]
{
(gridPosition + CornerTable[0] * size) * chunkScale,
(gridPosition + CornerTable[1] * size) * chunkScale,
(gridPosition + CornerTable[2] * size) * chunkScale,
(gridPosition + CornerTable[3] * size) * chunkScale
};
// Quad 추가
for (int i = 0; i < 6; i+=3)
{
int index0 = TriangleTable[15][i];
int index1 = TriangleTable[15][i + 1];
int index2 = TriangleTable[15][i + 2];
Vector3 vertex0 = quad[index0];
Vector3 vertex1 = quad[index1];
Vector3 vertex2 = quad[index2];
vertices.Add(vertex0);
vertices.Add(vertex1);
vertices.Add(vertex2);
int numTriangle = triangles.Count;
triangles.Add(numTriangle++);
triangles.Add(numTriangle++);
triangles.Add(numTriangle);
}
y += height;
}
}
대략적인 구현입니다. 각 Cell을 순회하면서 현재 Cell이 Quad라면 알고리즘이 시작됩니다. 최대한 늘릴 수 있는 만큼 Width와 Height를 계산한 뒤, Width와 Height크기의 Quad를 추가합니다. 여기에서 시각적인 자료를 찾아보실 수 있으니 참고하면 좋습니다.
결과
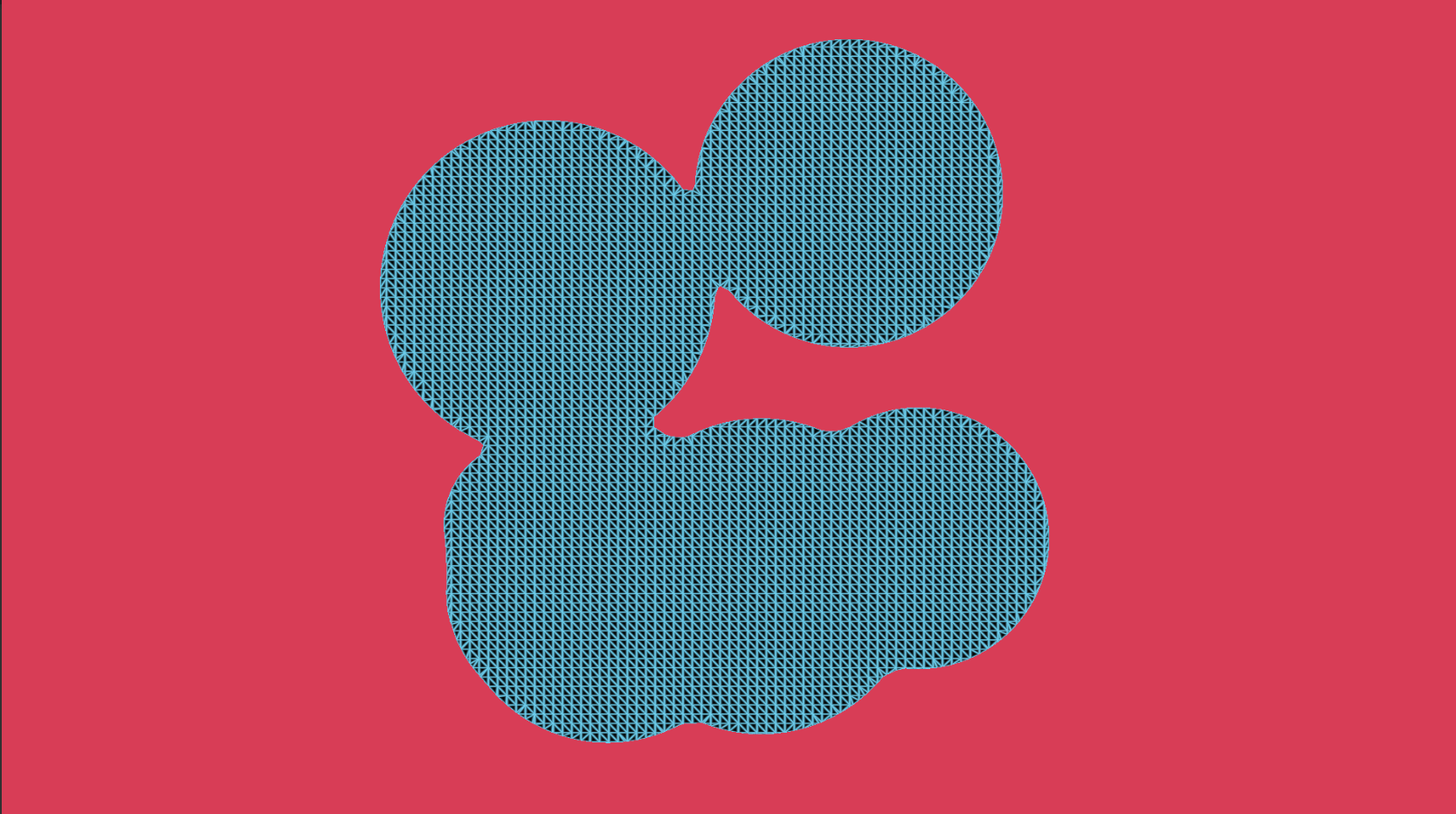
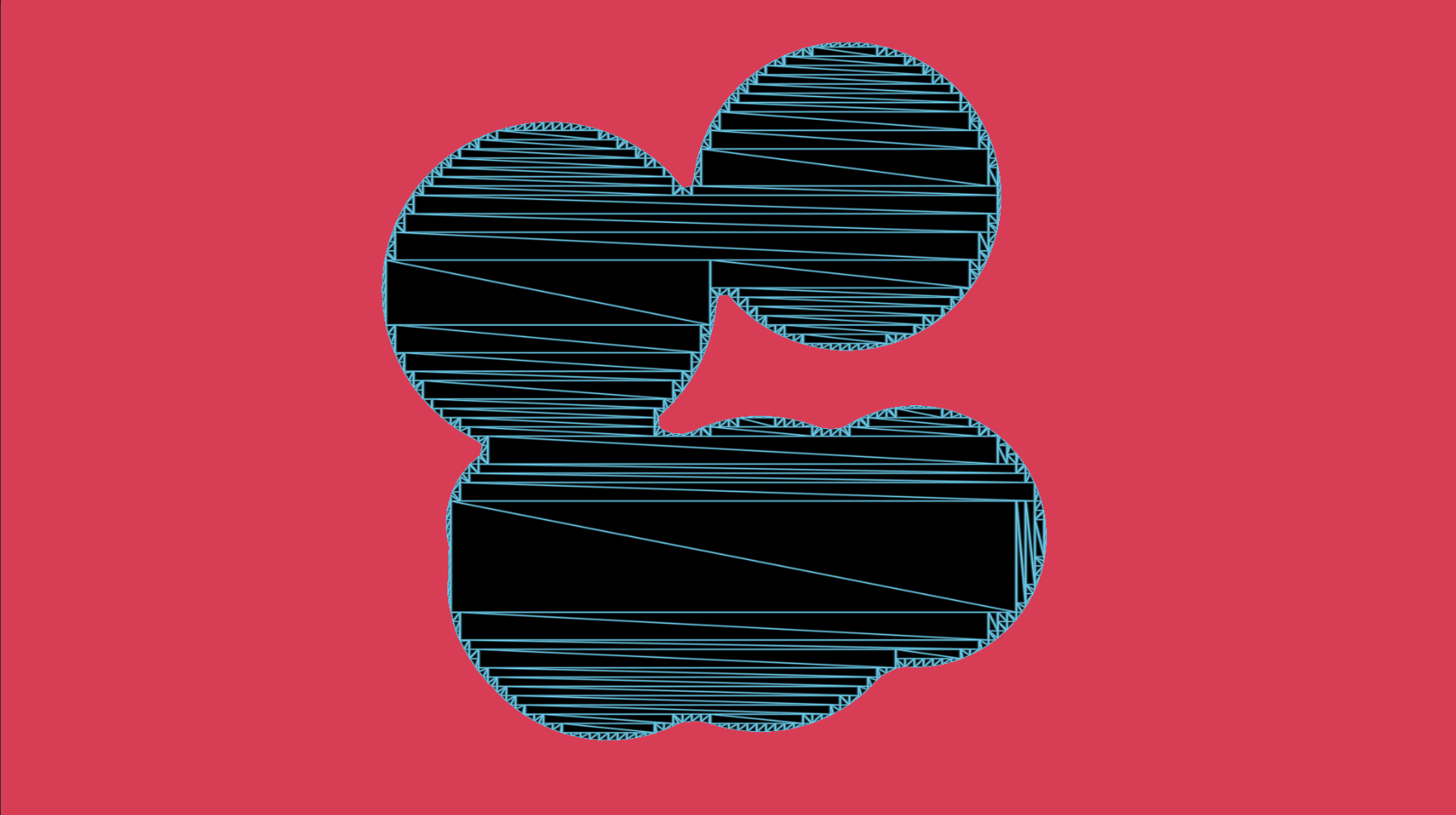
사실 최적의 방법은 아닙니다.
Unity Job System
ECS + Job System 예시 - 수많은 큐브도 끄떡없어요!
Unity의 C# Job system은 Unity C#으로 멀티스레드 코드를 작성할 수 있게 만든 시스템입니다. 쉽게말해서 멀티스레드 코드를 어렵지 않은 문법으로 작성하고, Unity에서 알아서 관리해주며, 경쟁 상태 등의 문제가 발생하지 않도록 잠재적인 경쟁 문제를 차단해줍니다. 자세한 이야기는 나중에 따로 포스팅을 하겠습니다.
하지만, 아직은 Preview 버전이라 API가 거의 Unity 버전 업마다 바뀌기 때문에, 관련 예제를 구글에서 찾아봐도 이전의 API를 사용하고 있어, 학습하기 어렵다는 문제가 있습니다. 그렇지만, 이정도 문제는 Job System을 사용해서 얻을 퍼포먼스를 생각하면 별거 아니라고 생각합니다.
결과
Job System 구현 결과
기존의 코드를 병렬처리 가능한 부분만 거의 동일하게 Job System을 이용하여 구현하였더니 43ms -> 2ms의 결과를 얻었습니다. 거의 20배의 성능 향상이 되었으니 성공적이라고 봐도 좋겠습니다.
마무리
Part 1에서부터 Part 3까지 걸쳐 Marching Squares 알고리즘을 살펴보았습니다. 위에서 다루지 않았던 자세한 구현은 Github/Marching-Squares에 있습니다. 다음에는 Marching Squares를 3차원으로 확장하여 Marching Cubes를 다뤄보겠습니다.
감사합니다.