PBR(물리 기반의 렌더링) 기본 정리

2020-02-21

Graphics
PBR

preview 하지만 수학과 물리는 몸에 해롭다

이 글은 제가 공부한 것을 정리한 글입니다. 따라서 잘못된 사실이 있거나 모호한 부분이 있다면 언제든지 댓글이나 메일을 보내주시면 감사하겠습니다.

Physically Based Rendering

PBR은 그전 Phong 이나 Blinn-Phong 같은 오래된 반사 모델과 달리 ‘조금 더’ 물리적으로 정확한 렌더링을 할 수 있습니다. 쉽게 말해서 물리적으로 그럴듯한 방식으로 더 사실적으로 표현하기 위한 방법이죠. PBR은 그전 오래된 반사 모델과 구별되는 큰 특징들을 가지고 있습니다.

Microfacet 표면 모델
에너지 보존 법칙
물리적 기반의 BRDF

위의 특징들을 살펴보기 전에 우선 렌더링 방정식에 대해 살펴보겠습니다.

Rendering Equation

Rendering Equation 점 $p$ 를 중심으로 하는 반구 $\Omega$ 내의 모든 들어오는 빛의 방향의 빛을 고려한다

PBR은 완전한 렌더링 방정식 대신 다음과 같은 단순화된 버전을 사용합니다.

$L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) (n \cdot \omega_i) d\omega_i$

이 무시무시해 보이는 식은 사실 그리 어렵진 않습니다. 간단히 설명하자면, 관측자가 점 $p$ 를 $\omega_o$ 의 방향으로 보았을 때의 Radiance $L_o(p,\omega_o)$ 는 반구 $\Omega$ 로 $\omega_i$ 방향으로 들어오는 빛의 Radiance를 모두 합한 것입니다. 표면에 직각으로 빛이 들어올 때 가장 강한데, 이를 표현하는 식이 $n \cdot \omega_i$ 입니다. $f_r(p,\omega_i,\omega_o)$ 는 Bidirectional reflectance distribution function, BRDF라고 부르는데, 앞으로 차근차근 살펴보겠습니다.

Microfacet 표면 모델

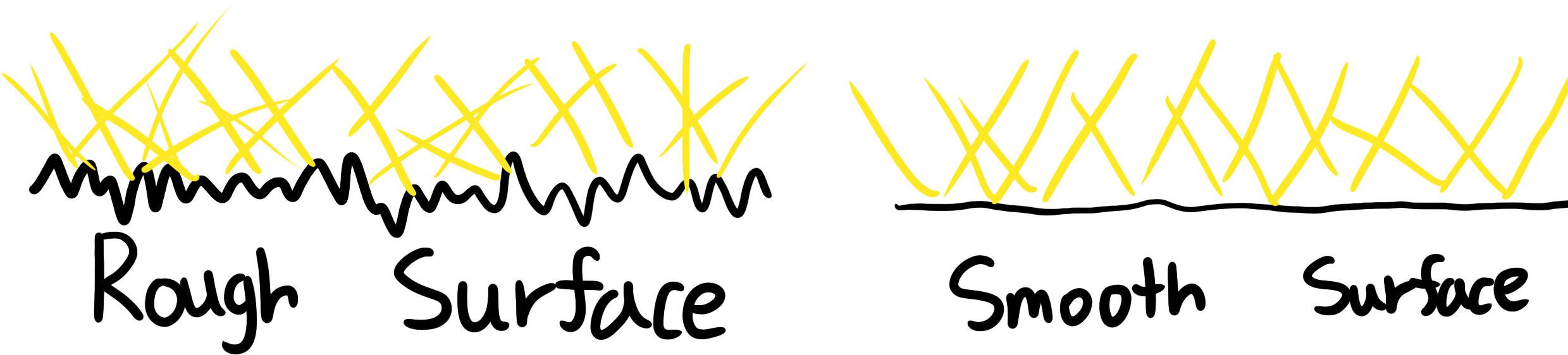Rough and Smooth 부드러운 표면은 거울과 같아진다

모든 물리 기반의 PBR 모델은 Microfacet 이론을 기반으로 합니다. Microfacet 표면 모델이란, Macrofacet은 아주 미세한 Microfacet들을 가지고, 이 Microfacet들은 완벽한 거울입니다. PBR에서는 표면이 거친 정도를 표현하는 파라미터인 Roughness를 사용해 Microfacet들이 얼마나 표면과 정렬되어있는지 표현합니다. 실제로 위 그림을 보면 왼쪽의 거친 표면에서는 매우 불규칙하게 산란하고, 왼쪽의 매끄러운 표면에서는 표면의 실제 노말과 거의 정렬되어 반사가 발생하고 있습니다.

에너지 보존 법칙

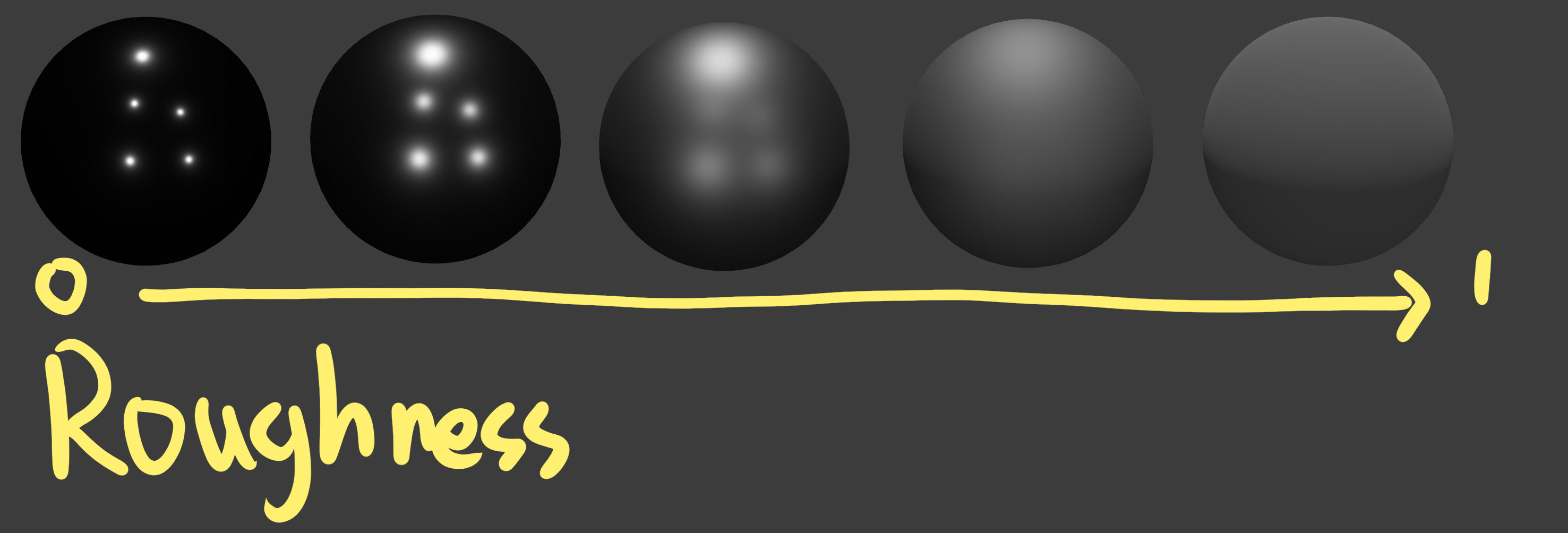Roughness가 증가함에 따라 점점 밝아진다

PBR은 에너지 보존 법칙을 만족합니다. 즉, 나가는 빛 에너지는 들어오는 빛 에너지보다 클 수 없다는 이야기죠. 위 이미지를 보시면 왼쪽에서 오른쪽으로 갈수록 점점 더 색이 옅어지는 것을 알 수 있습니다. 만약 Specular의 모양이나 크기와 관계없이 색이 일정하다면 거친 표면에서는 더 많은 에너지를 방출하는 것이므로 이는 에너지 보존 법칙에 위배된다고 볼 수 있습니다. 따라서 오른쪽으로 갈수록 점점 더 색이 옅어지는 것입니다.

물리적 기반의 BRDF

BRDF는 들어오는 빛의 방향 $w_i$ , 나가는 빛의 방향 $\omega_o$ , 표면의 노말 $n$ , 표면의 파라미터 $a$ 를 입력으로 하는 함수입니다. 이를 입력으로 하여 물질의 특성을 고려해 불투명한 표면의 최종 반사광에 얼마나 많은 기여를 했는지 결과로 계산하게 됩니다. 만약 표면이 거울과 같은 완전히 매끄러운 표면이라면 BRDF 함수는 모든 $w_i$ 에 대해서 0을 반환하고 $\omega_o$ 에 대해 1을 반환합니다.

Cook-Torrance BRDF

Cook-Torrance BRDF는 Unreal Engine 4나 Unity와 같은 유명한 상용엔진에서도 사용하는 BRDF입니다. Cook-Torrance BRDF는 다음과 같이 Diffuse와 Specular로 나뉩니다.

$f_r = k_d f_{lambert} + k_s f_{cook-torrance}$

Diffuse 파트 $f_{lambert}$

$k_d$ 는 들어오는 빛의 비율이며 $k_s$ 는 반사되어 나가는 빛의 비율입니다. $f_{lambert}$ 는 램버트 반사율을 표현하는데, 이는 물체 표면의 휘도가 등방성을 가질 때를 의미한다고 합니다. 쉽게 말해서 관찰자가 바라보는 각도와 관계없이 모두 같은 색이 보인다는 것이죠. 실제로 나무와 같은 원목 재질은 각도에 따라 밝기가 크게 변하지 않아 거의 램버트 반사율을 가지지만, 금속이 포함된 물건은 광원의 위치에 따라 반짝이는 부분이 보일 수 있습니다.

$k_{lambert} = \frac{c}{\pi}$

$c$ 는 Albedo 또는 표면의 색입니다. 보통 물체의 색을 표현하는 Albedo Texture에서 값을 받아옵니다. 위에서 살펴보았던 렌더링 방정식에서 램버트만을 고려한다면 다음과 같이 쓸 수 있습니다.

$L_o(p,\omega_o) = \int\limits_{\Omega} k_d f_{lambert} (n \cdot \omega_i) d\omega_i$

이때 $k_d$ 와 $k_{lambert}$ 는 적분과 관계가 없으므로 앞으로 나올 수 있습니다.

$L_o(p,\omega_o) = k_d f_{lambert} \int\limits_{\Omega}(n \cdot \omega_i) d\omega_i$

즉, $k_{lambert}$ 는

$k_{lambert} = \frac{L_o(p,\omega_o)}{k_d \int\limits_{\Omega}n \cdot \omega_i d\omega_i}$

$n \cdot \omega_i$ 에서 $n$ 과 $\omega_i$ 는 길이가 1로 정규화하여 쓰기 때문에 $cos\theta$ 로 바꿀 수 있습니다.

$\int_{\Omega}cos\theta d\omega_i = \pi$

따라서

$k_{lambert} = \frac{c}{\pi}$

이것이 $k_{lambert}$ 를 구하기 위해 $\pi$ 로 나누는 이유입니다.

Specular 파트 $f_{cook-torrance}$

$f_{cook-torrance} = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}$

Cook-Torrance의 Specular BRDF는 3가지 함수와 이를 정규화하는 계산으로 이루어집니다. 각각 Normal Distribution Function, Fresnel Equation, Geometry Function입니다.

Normal Distribution Function : 표면의 거칠기에 따라 Microfacet들이 얼마나 $H$ 벡터와 정렬되는지 계산합니다.
Geometry Function : Microfacet으로 인한 Occlusion으로 Shadowing과 Masking이 발생해 표면이 반사하는 빛을 줄일 수 있습니다.
Fresnel Equation : 서로 다른 각도의 표면에서 반사되는 빛의 비율을 나타냅니다.

$D$ : Trowbridge-Reitz GGX

$NDF_{Trowbridge-Reitz GGX}(n, h, \alpha) = \frac{\alpha^2}{\pi((n \cdot h)^2 (\alpha^2 - 1) + 1)^2}$

$D$ 는 표면의 Microfacet들 중 $H$ 벡터에 정확히 정렬된 Microfacet들이 얼마나 있는지 통계적으로 근사한 함수입니다.

Half Vector

Half Vector Microfacet을 샘플링 해보기

표면의 Microfacet들은 모두 다른 노말을 가지고 있습니다. 또한 앞서 이야기했듯이 Microfacet은 거울면 반사가 일어납니다. 거울면 반사란 입사각과 반사각이 같은 반사입니다. 즉, $H$ 와 $m$ 이 일치하는 경우에 거울면 반사가 일어납니다. 이때 생각할 수 있는 것은 표면이 거칠다면 난반사가 심해질 것이고, 부드럽다면 정반사가 커질 것입니다. 따라서 $D$ 는 $H$ 와 $m$ 의 각도가 0이 되는 Microfacet의 분포를 찾는 함수입니다.

Normal Distribution Function Example Roughness가 높아지면 NDF가 낮아진다

Roughness가 높으면, 즉 표면이 거칠수록 Microfacet의 노말 $m$ 과 $H$ 가 정렬되지 않아 Specular가 흐릿해지는 현상을 볼 수 있습니다. 역시 표면이 부드러우면 $m$ 과 $H$ 가 정렬되기 때문에 NDF가 높아 Specular가 매우 밝아집니다.

float DistributionTrowbridgeReitzGGX(vec3 normal, vec3 halfDir, float roughness)
{
	float alpha = roughness * roughness;
	float alpha2 = alpha * alpha;
	float NdotH = saturate(dot(normal, halfDir));

	float num = alpha2;
	float denom = PI * pow(NdotH * NdotH * (alpha2 - 1) + 1, 2);

	return num / denom;
}

$G$ : SchlickGGX + SmithsMethod

Masking and Shadowing Microfacet이 거칠수록 빛이 온전히 반사되지 않는다

$G_{SchlickGGX}(n, v, k) = \frac{n \cdot v} {(n \cdot v)(1 - k) + k }$

$G$ 는 표면의 Microfacet들이 서로 겹쳐서 빛이 차단되는 영역을 통계적으로 근사한 함수입니다. $G$ 가 0이면 다른 Microfacet이 완전히 빛을 막는 것이고, $G$ 가 1이면 Microfacet으로 인해 막히는 빛이 없다는 뜻입니다. 이때 $k$ 는 $alpha$ 를 다시 매핑한 것입니다.

$k = \frac{\alpha}{2}$

$alpha$ 는 다음과 같이 계산됩니다.

$\alpha = (\frac{Roughness + 1}{2})^2$

하지만 Disney에 따르면 Roughness에 따른 ‘hotness’를 줄이기 위해 식을 다음과 같이 고쳤다고 합니다.

$k = \frac{(Roughness + 1)^2}{8}$

float GeometrySchlickGGX(vec3 normal, vec3 v, float k)
{
	k += 1;
	k = (k * k) / 8.0; // Direct Lighting Remapped
	float NdotV = saturate(dot(normal, v));

	float num = NdotV;
	float denom = NdotV * (1 - k) + k;

	return num / denom;
}

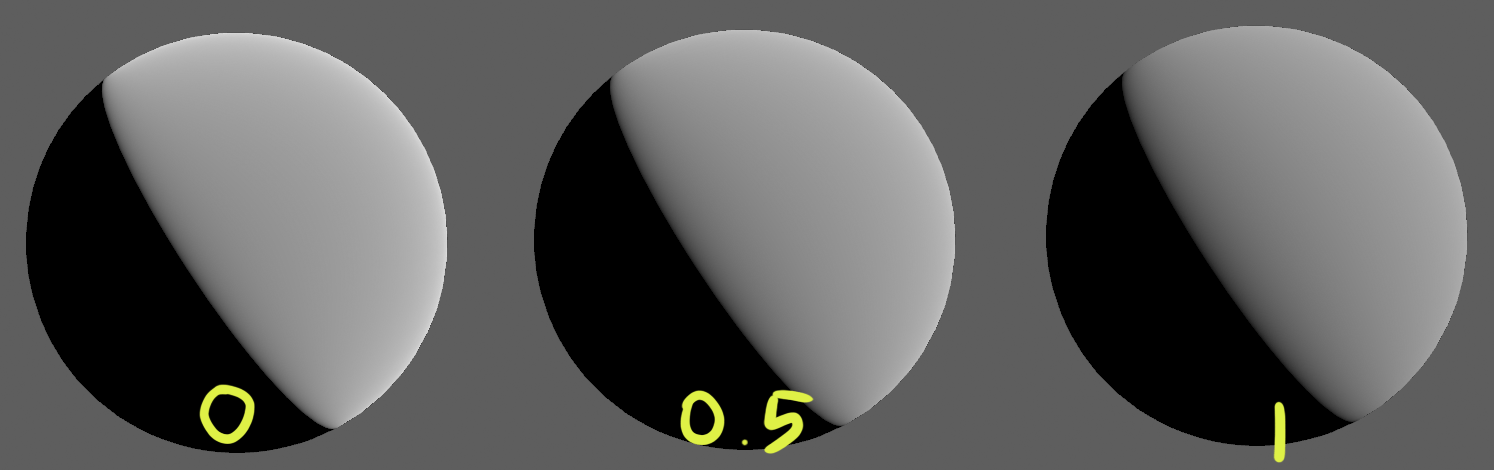Geometry Function 표면이 거칠어질수록 빛이 차단되는 정도가 커진다

표면을 효과적으로 근사하기 위해서는 관찰자가 바라보는 방향인 $v$ 와 빛의 방향인 $l$ 를 모두 고려해야 합니다. 따라서 Smiths의 방법을 이용해서 해결할 수 있습니다.

$G(n, v, l, k) = G_{sub}(n, v, k) G_{sub}(n, l, k)$

float GeometrySmithsMethod(vec3 normal, vec3 viewDir, vec3 lightDir, float k)
{
	float viewSub = GeometrySchlickGGX(normal, viewDir, k);
	float lightSub = GeometrySchlickGGX(normal, lightDir, k);
	return viewSub * lightSub;
}

$F$ : Schlick Approximation

Fresnel Effect of Real World 물체를 90도에 가깝게 볼수록 Specular가 더 밝아진다

$F$ 는 표면을 보는 각도에 따라 빛을 얼마나 반사할지 정하는 함수입니다. 모든 물질은 표면을 정면에서 똑바로 본다면 원래 반사하는 만큼을 볼 수 있지만, 거의 90도 각도로 물체를 보게 된다면 보다 더 밝게 Specular가 보입니다. 이것이 바로 Fresnel 현상입니다. 실제로 위 이미지에서 좌측은 편광필터로 Diffuse만 뽑은 것이고, 우측은 Specular만 뽑은 이미지입니다. 우측의 Specular가 90도에 가깝게 관찰을 할수록 더 밝게 보인다는 것을 볼 수 있습니다.

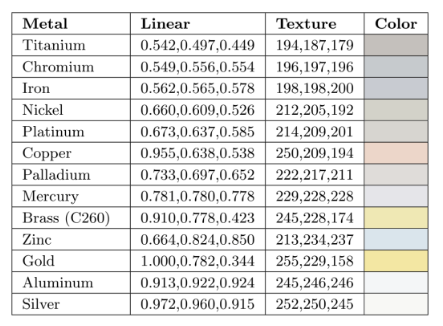Fresnel Effect of Real World Naty Hoffman의 Real-Time Rendering, Fourth Edition에서

$F_{Schlick}(h, v, F_0) = F_0 + (1 - F_0) ( 1 - (h \cdot v))^5$

$F_0$ 는 표면의 기본 반사율입니다. 보통 $IOR$ 을 1.5로 사용하는데 이를 계산해보면 $F_0$ 가 0.04입니다. $F_0$ 는 다음과 같이 계산할 수 있습니다.

$F_0 = (\frac{IOR-1}{IOR+1})^2$ $F_0(1.5) = (\frac{1.5 - 1}{1.5 + 1})^2 = 0.04$

Fresnel 90도에 가까워질수록 빛을 반사하는 정도가 더 커진다

vec3 FresnelSchlickApproximation(vec3 F0, vec3 viewDir, vec3 halfDir)
{
	float HdotV = saturate(dot(halfDir, viewDir));
	return F0 + (1.0 - F0) * pow(1.0 - HdotV, 5);
}

모두 합해서

$L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i$

위의 항들을 모두 합하면 다음과 같이 방정식을 다시 쓸 수 있습니다. 이때 자세히 보시면 $f_{cook-torrance}$ 부분 앞에 $k_s$ 가 없는 것을 알 수 있습니다. 이는 $F$ 가 표면에서 반사되는 빛의 비율을 나타내므로 $F$ 가 $k_s$ 를 포함하고 있기 때문입니다.

유용한 링크

코드 (Git Repository)

learnopengl PBR Theory

Deriving-Lambertian-BRDF-From-First-Principles

2012 pbs disney brdf notes

2013 Siggraph Presentations Notes

PBR Online Book

2010 Siggraph Course Notes

 OpenGL 개발 이슈 - glUniform Lambertian과 Oren Nayar 알아보기 